Dave's Math Tables: Log Expansions 
(Math | Calculus | Expansions | Series | Log)

Expansions of the Logarithm Function
Function Summation Expansion Comments
  ln (x)
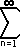=sum (n=1..inf)  (x-1)n 
n 
= (x-1) - (1/2)(x-1)2 + (1/3)(x-1)3 + (1/4)(x-1)4 + ...		 Taylor Series Centered at 1 
(0 < x <=2)
  ln (x)
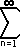=sum (n=1..inf)  ((x-1) / x)n 
n 
 = (x-1)/x + (1/2) ((x-1) / x)2 + (1/3) ((x-1) / x)3 + (1/4) ((x-1) / x)4 + ... 
 		 (x > 1/2)
  ln (x)
=ln(a)+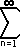sum (n=1..inf)  (x-a)n 
n an 
 = ln(a) + (x-a) / a - (x-a)2 / 2a2 + (x-a)3 / 3a3 - (x-a)4 / 3a4 + ... 		 Taylor Series 
(0 < x <= 2a)
  ln (x)
=2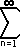sum (n=1..inf) ((x-1)/(x+1))(2n-1) 
(2n-1) 
 = 2 [ (x-1)/(x+1)  + (1/3)( (x-1)/(x+1) )3 + (1/5) ( (x-1)/(x+1) )5 + (1/7) ( (x-1)/(x+1) )7 + ... ] 		 (x > 0)

Expansions Which Have Logarithm-Based Equivalents
Summantion Expansion Equivalent Value Comments
sum (n=1..inf) x n 
n
 = x + (1/2)x2  +(1/3)x3 + (1/4)x4 + ...		 = - ln (x + 1) (-1 < x <= 1)
sum (n=1..inf) (-1)n xn 
n
 = - x + (1/2)x2 - (1/3)x3 + (1/4)x4 + ...		 = - ln(x) (-1 < x <= 1)
sum (n=1..inf) x2n-1 
2n-1
 = x + (1/3)x3 + (1/ 5)x5 + (1/7)x7 + ...		 = ln ( (1+x)/(1-x) ) 
2		 (-1 < x < 1)
 
 

Casa de Bender