
Tablas Matemáticas de David: La Serie Fourier  |
| (Matemática | Advanzado | Serie Fourier) |
 La serie de fourier de la función f(x)
La serie de fourier de la función f(x)
a(0) / 2 +
el residuo(n) = f(x) - Sn(x) = 1/PI
Sn(x) = 1/PI
lim(k->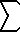 (k=1..
(k=1..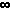 ) (a(k) cos kx + b(k) sin kx)
) (a(k) cos kx + b(k) sin kx)
a(k) = 1/PI

 f(x) cos kx dx
f(x) cos kx dx
b(k) = 1/PI 
 f(x) sin kx dx
f(x) sin kx dx
 El residuo de la serie de fourier. Sn(x) = la suma de los primeros n+1 términos a x.
El residuo de la serie de fourier. Sn(x) = la suma de los primeros n+1 términos a x.
 f(x+t) Dn(t) dt
f(x+t) Dn(t) dt
 f(x+t) Dn(t) dt
f(x+t) Dn(t) dt
Dn(x) = Dirichlet kernel = 1/2 + cos x + cos 2x + .. + cos nx = [ sin(n + 1/2)x ] / [ 2sin(x/2) ]
 Teorema de Riemann. Si f(x) es continuo a excepción de un número finito de saltos finitos en todos los intervalos finitos pues:
Teorema de Riemann. Si f(x) es continuo a excepción de un número finito de saltos finitos en todos los intervalos finitos pues: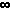 )
) 
 f(t) cos kt dt = lim(k->
f(t) cos kt dt = lim(k->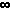 )
)
 f(t) sin kt dt = 0
f(t) sin kt dt = 0
 La serie fourier del función f(x) en un intervalo arbitrario.
La serie fourier del función f(x) en un intervalo arbitrario.
A(0) / 2 +
1/PI 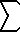 (k=1..
(k=1..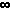 ) [ A(k) cos (k(PI)x / m) + B(k) (sin k(PI)x / m) ]
) [ A(k) cos (k(PI)x / m) + B(k) (sin k(PI)x / m) ]
a(k) = 1/m

 f(x) cos (k(PI)x / m) dx
f(x) cos (k(PI)x / m) dxb(k) = 1/m

 f(x) sin (k(PI)x / m) dx
f(x) sin (k(PI)x / m) dx El Teorema de Parseval. Si f(x) es continuo; f(-PI) = f(PI) pues
El Teorema de Parseval. Si f(x) es continuo; f(-PI) = f(PI) pues
 f^2(x) dx = a(0)^2 / 2 +
f^2(x) dx = a(0)^2 / 2 + 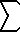 (k=1..
(k=1..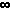 ) (a(k)^2 + b(k)^2)
) (a(k)^2 + b(k)^2)
 La Integral Fourier del función f(x)
La Integral Fourier del función f(x)
f(x) = 
 ( a(y) cos yx + b(y) sin yx ) dy
( a(y) cos yx + b(y) sin yx ) dy
a(y) = 1/PI

 f(t) cos ty dt
f(t) cos ty dtb(y) = 1/PI
f(x) = 1/PI 
 f(t) sin ty dt
f(t) sin ty dt
 dy
dy 
 f(t) cos (y(x-t)) dt
f(t) cos (y(x-t)) dt
 Casos Espaciales de la Integral Fourier
Casos Espaciales de la Integral Fourier
si f(x) = f(-x) pues
f(x) = 2/PI
if f(-x) = -f(x) then

 cos xy dy
cos xy dy 
 f(t) cos yt dt
f(t) cos yt dtf(x) = 2/PI

 sin xy dy
sin xy dy 
 sin yt dt
sin yt dt (Transforms) de Fourier
(Transforms) de Fourier
(Transform) Fourier Coseno
g(x) = 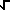 (2/PI)
(2/PI)
 f(t) cos xt dt
f(t) cos xt dt
(Transform) Fourier Seno
g(x) = 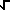 (2/PI)
(2/PI)
 f(t) sin xt dt
f(t) sin xt dt
 Identidades de los (tranforms)
Identidades de los (tranforms)
Si f(-x) = f(x) pues
Transform Fourier Coseno ( Tranform Fourier Coseno (f(x)) ) = f(x)
Si f(-x) = -f(x) pues
Transform Fourier Seno (Transform Fourier Seno (f(x)) ) = f(x)
