
Tablas Matemáticas de David: Identidades de Diferenciación  |
| (Matemática | Cálculo | Derivadas | Identidades) |
Definiciones de la Derivada:
df / dx = lim (dx -> 0) (f(x+dx) - f(x)) / dx (derecho)
df / dx = lim (dx -> 0) (f(x) - f(x-dx)) / dx (izquierdo)
df / dx = lim (dx -> 0) (f(x+dx) - f(x-dx)) / (2dx) (ambos lados)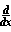

 f(t) dt = f(x) (Teorema Fundamental para Derivadas)
f(t) dt = f(x) (Teorema Fundamental para Derivadas)
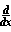 c f(x) = c
c f(x) = c
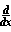 f(x) (c es un constante)
f(x) (c es un constante)
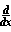 (f(x) + g(x)) =
(f(x) + g(x)) =
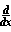 f(x) +
f(x) + 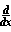 g(x)
g(x)
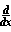 f(g(x)) =
f(g(x)) = 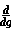 f(g) *
f(g) * 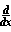 g(x) (regla de la cadena)
g(x) (regla de la cadena)
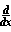 f(x)g(x) = f'(x)g(x) + f(x)g '(x) (regla de producto)
f(x)g(x) = f'(x)g(x) + f(x)g '(x) (regla de producto)