
Tablas Matemáticas de David: Vectores  |
| (Matemática | Cabos Sueltos | Vectores) |
Notación: Las letras minúsculas a-h, l-z denotan escalares. Las letras mayúsculas y negritas A-Z denotan vectores. Letras minúsculas y negritas i, j, k denotan vectores de unidad. <a, b> denota un vector con componentes a y b. <x1, .., xn> denota un vector con n componentes cuales son x1, x2, x3, ..,xn. |R| denota la magnitud del vector R.
|<a, b>| = la magnitud del vector = 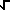 (a 2+ b 2)
(a 2+ b 2)
|<x1, .., xn>| = 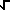 (x1 2+ .. + xn 2)
(x1 2+ .. + xn 2)
<a, b> + <c, d> = <a+c, b+d>
<x1, .., xn> + <y1, .., yn>= < x1+y1, .., xn+yn>
k <a, b> = <ka, kb>
k <x1, .., xn> = <k x1, .., k x2>
<a, b>  <c, d> = ac + bd
<c, d> = ac + bd
<x1, .., xn>  <y1, ..,yn> = x1 y1 + .. + xn yn>
<y1, ..,yn> = x1 y1 + .. + xn yn>
R  S= |R| |S| cos
S= |R| |S| cos  (
( = el ángulo entre los)
= el ángulo entre los)
R  S= S
S= S  R
R
(a R)  (bS) = (ab) R
(bS) = (ab) R  S
S
R  (S + T)= R
(S + T)= R  S+ R
S+ R  T
T
R  R = |R| 2
R = |R| 2
|R x S| = |R| |S| sen  (
( = el ángulo entre los dos vectores). La dirección de R x S es perpendicular a A & B y según a la ley de mano derecha.
= el ángulo entre los dos vectores). La dirección de R x S es perpendicular a A & B y según a la ley de mano derecha.
| i j k |
R x S = | r1 r2 r3 | = / |r2 r3| |r3 r1| |r1 r2| \
| s1 s2 s3 | \ |s2 s3| , |s3 s1| , |s1 s2| /
S x R = - R x S
(a R) x S = R x (a S) = a (Rx S)
R x (S + T) = R x S + Rx T
R x R = 0
Si a, b, c = los ángulos entre los vectores de unidad i, j,k y R Pues los cosenos de dirección son definidos por:
cos a = (R  i) / |R|; cos b = (R
i) / |R|; cos b = (R  j) / |R|; cos c = (R
j) / |R|; cos c = (R  k) / |R|
k) / |R|
|R x S| = El área del paralelográmo con lados R y S.
El componente de R en la dirección de S = |R|cos  = (R
= (R S) / |S| (resultado escalar)
S) / |S| (resultado escalar)
El proyección de R el la dirección de S = |R|cos  = (R
= (R S) S/ |S| 2 (resultado vector)
S) S/ |S| 2 (resultado vector)
