
Dave's Math Tables: Fourier Transforms  |
| (Math | Advanced | Transforms | Fourier) |
Fourier Transform
 Definition of Fourier Transform
Definition of Fourier Transformf(x) = 1/
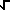 (2
(2 )
) 
 g(t) e^(i tx) dt
g(t) e^(i tx) dt Inverse Identity of Fourier Transform
Inverse Identity of Fourier Transformg(x) = 1/
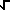 (2
(2 )
) 
 f(t) e^(-i tx) dt
f(t) e^(-i tx) dt
Fourier Sine and Cosine Transforms
 Definitions of the Transforms
Definitions of the Transformsf(x) =
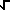 (2/
(2/ )
) 
 g(x) cos(xt) dt (Cosine Transform)
g(x) cos(xt) dt (Cosine Transform)
f(x) = 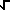 (2/
(2/ )
) 
 g(x) sin(xt) dt (Sine Transform)
g(x) sin(xt) dt (Sine Transform) Identities of the Transforms
Identities of the TransformsIF f(x) is even, THEN FourierSineTransform( FourierSineTransform(f(x)) ) = f(x)
IF f(x) is odd, THEN FourierCosineTransform( FourierCosineTransform(f(x)) ) = f(x)
Under certain restrictions of continuity.

Casa de Bender